學習資源

https://labuladong.online/algo/data-structure-basic/binary-tree-basic/

學習記錄

今天是學習的第 19 天，主要學習了二叉樹基礎及常見類型：

二叉樹是最重要的基本資料結構，很多複雜的資料結構都是建立在二叉樹的基礎上。所以把二叉樹搞懂了，後面學其他東西會輕鬆很多。

二叉樹的基本介紹

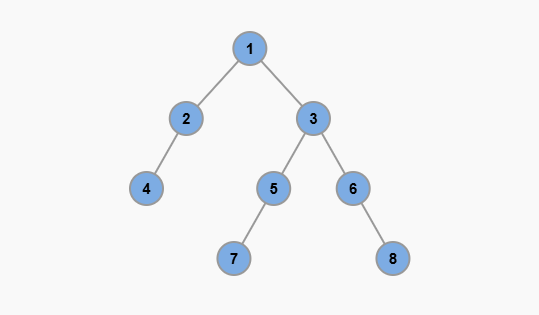
1. 子節點和父節點：每個節點下面直接連接的就叫子節點（像節點 4 就是節點 2 的子節點），上面那個就叫父節點（節點 2 是節點 4 的父節點）。
2. 子樹：以某個子節點為起點的整棵樹，就叫做子樹（比如節點 5 和 7 這一塊，就是節點 3 的左子樹）。
3. 根節點和葉子節點：最上面的節點 1 叫做根節點，最下面沒有子節點的節點 4、7、8 叫做葉子節點。
4. 深度/高度：從根節點走到最底層要經過幾個節點，這個數字就是樹的深度。上面這棵樹的深度是 4。

滿二叉樹

滿二叉樹就是每一層節點都是滿的，整棵樹就像一個三角形：

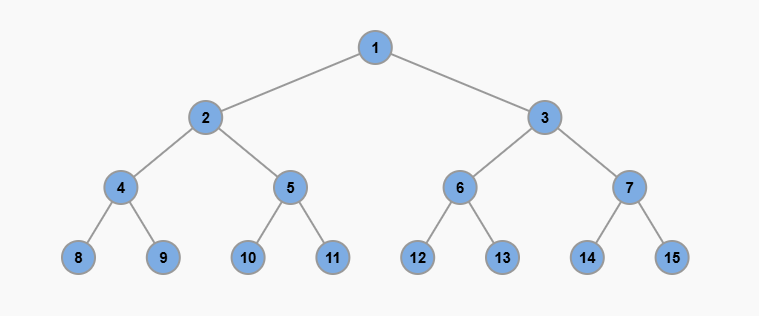
有個小技巧：如果滿二叉樹的深度是 h，節點總數就是 2^h - 1。所以上面這棵深度 4 的樹，節點數就是 2^4-1=15 個。

完全二叉樹

完全二叉樹的規則是：每一層的節點都要靠左排列，而且除了最後一層，其他層都必須是滿的：

二叉搜索樹

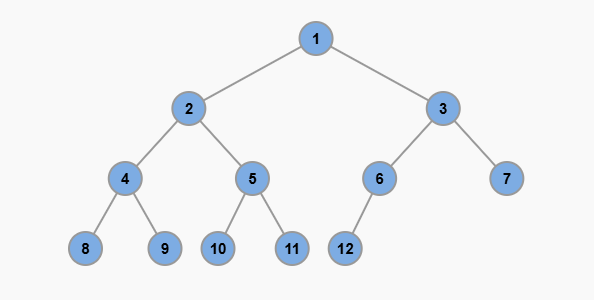
二叉搜索樹有個簡單的口訣：「左小右大」

意思就是說，對於每個節點：

• 左邊子樹的所有節點都要比它小
• 右邊子樹的所有節點都要比它大

高度平衡二叉樹

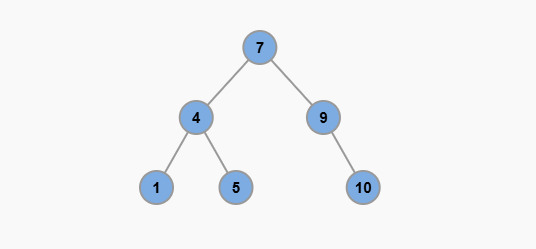
高度平衡二叉樹的特點是：每個節點的左右子樹高度差都不能超過 1。

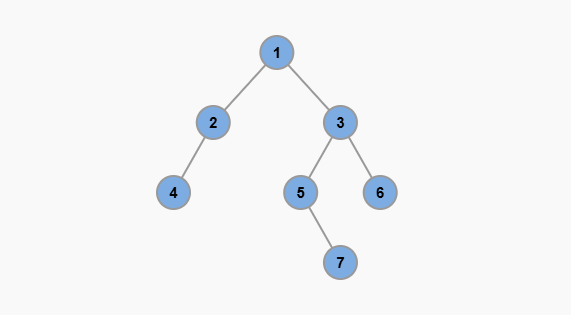
這樣做有什麼好處呢？假設樹裡有 N 個節點，那麼樹的高度就能保持在 O(log n)。

自平衡二叉樹

自平衡二叉樹是在增刪二叉樹節點的時候，對樹結構進行調整，讓樹的高度始終保持平衡。

二叉樹的實現方式

方法一：鏈表結構（最常見）

每個節點都有指向左右子節點的指針：

var TreeNode = function(x) {
    this.val = x;
    this.left = null;
    this.right = null;
}

// 構建一棵二叉樹：
var root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.right.left = new TreeNode(5);
root.right.right = new TreeNode(6);

// 構建出來的二叉樹是這樣的：
//     1
//    / \
//   2   3
//  /   / \
// 4   5   6

方法二：哈希表

其中鍵是父節點 id，值是子節點的 id 列表：

// 1 -> [2, 3]
// 2 -> [4]
// 3 -> [5, 6]

let tree = new Map([
    [1, [2, 3]],
    [2, [4]],
    [3, [5, 6]]
]);

學習總結

• 很多複雜的資料結構都是建立在二叉樹的基礎上
• 有幾種常見的二叉樹類型：
  • 滿二叉樹
  • 完全二叉樹
  • 二叉搜索樹
  • 高度平衡二叉樹
  • 自平衡二叉樹
• 二叉樹可以用鏈表或是哈希表來構建